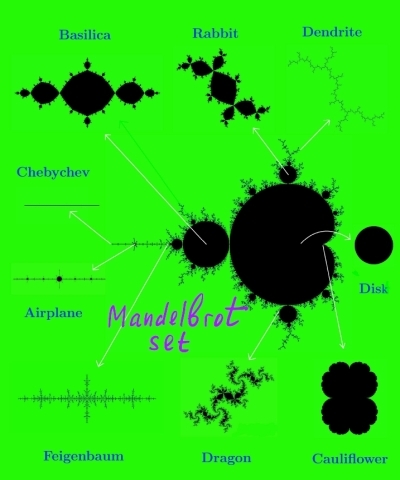
The Mandelbrot set M is a fascinating fractal that encodes in one image the dynamical complexity of the quadratic family z^2 + c. We will wander around M, trying to make sense of its bubbles and their bifurcations, explain how baby Mandelbrot sets are born and where the herds of elephants march, along with various other observable features of M. Despite its enormous complexity, there is a good chance of obtaining a precise topological and geometric description of M. It depends, though, on confirming a long-standing “MLC Conjecture” (on the local connectivity of M) and building up several “Renormalization Theories” that control the small-scale structure of this set.