The aim of this talk is to give an overview of some recent results in two interconnected areas:
a) Random graphs and complex networks: The last decade of the 20th century saw significant growth in the availability of empirical data on networks, and their relevance in our daily lives. This stimulated activity in a multitude of fields to formulate and study models of network formation and dynamic processes on networks to understand real-world systems.
One major conjecture in probabilistic combinatorics, formulated by statistical physicists using non-rigorous arguments and enormous simulations in the early 2000s, is as follows: for a wide array of random graph models on
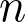
vertices and degree exponent
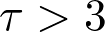
, typical distance both within maximal components in the critical regime as well as on the minimal spanning tree on the giant component in the supercritical regime scale like
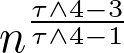
. In other words, the degree exponent determines the universality class the random graph belongs to. The mathematical machinery available at the time was insufficient for providing a rigorous justification of this conjecture.
More generally, recent research has provided strong evidence to believe that several objects, including
(i) components under critical percolation,
(ii) the vacant set left by a random walk, and
(iii) the minimal spanning tree,
constructed on a wide class of random discrete structures converge, when viewed as metric measure spaces, to some random fractals in the Gromov-Hausdorff-Prokhorov sense, and these limiting objects are universal under some general assumptions. We report on recent progress in proving these conjectures.
b) Stochastic geometry: In contrast, less precise results are known in the case of spatial systems. We discuss a recent result concerning the length of spatial minimal spanning trees that answers a question raised by Kesten and Lee in the 90's, the proof of which relies on a variation of Stein's method and a quantification of the classical Burton-Keane argument in percolation theory.
Based on joint work with Louigi Addario-Berry, Shankar Bhamidi, Nicolas Broutin, Sourav Chatterjee, Remco van der Hofstad, and Xuan Wang.